Chan-algoritmus

A Timothy M. Chanról elnevezett Chan-algoritmus optimális kimenetérzékeny algoritmus, amellyel egy $n$ pontot tartalmazó $P$ halmaz konvex burkát lehet kiszámítani 2- és 3-dimenziós térben. A kiszámításhoz $O(n\log h)$ idő szükséges, ahol $h$ a konvex burok csúcsainak száma. A kétdimenziós esetben egy $O(n\log n)$ algoritmust (például a Graham-féle pásztázást) és a Jarvis-féle menetelést ($O(nh)$) kombinálja az optimális $O(n\log h)$ futásidő eléréséhez. A Chan-algoritmus arról nevezetes, hogy sokkal egyszerűbb, mint a Kirkpatrick–Seidel-algoritmus, és egyszerűen kiterjeszthető a háromdimenziós térbe is. Ezt a modellt Chantól függetlenül Frank Nielsen is kifejlesztette a Ph.D. disszertációjában.

A Chan-algoritmus 2-dimenziós esetben. Itt a pontokat x-koordináta alapján osztottuk szét, míg az igazi algoritmus tetszőleges szétosztásra is működik.

Algoritmus

Áttekintés

Az algoritmus sikeres lefutásához egyetlen $m\geq h$ paraméterre van szükség. Tegyük fel, hogy ez egy fix érték (a valóságban $h$-t nem ismerjük előre, ezért több, egyre növekvő értékű $m$ paramétert használunk, lásd később).

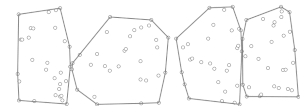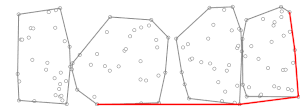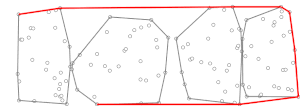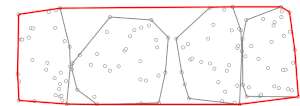
Az algoritmus első lépése a $P$ halmaz tetszőleges szétosztása $K\leq 1+n/m$ darab részhalmazra $(Q_{k})_{k=1,2,...K}$, mindben legfeljebb $m$ ponttal. Ekkor $K=O(n/m)$.

Ezután az első fázisban egy $O(p\log p)$ algoritmus segítségével (például Graham-féle pásztázás) minden $Q_{k}$-ra kiszámítja a részhalmaz konvex burkát, $C_{k}$-t, ahol $p$ a részhalmaz pontjainak száma. Mivel $K$ részhalmaz van és mindegyikben $O(m)$ pont, ez a fázis $K\cdot O(m\log m)=O(n\log m)$ időt vesz igénybe.

A második fázisban az algoritmus a Jarvis-féle menetelést hajtja végre, a már kiszámított kis konvex burkok $(C_{k})_{k=1,2,...K}$ felhasználásával. Ennek során minden lépésben veszünk egy $p_{i}$ pontot, amely a konvex burok része (először $p_{i}$ lehet a $P$ halmaz legalacsonyabb $y$ koordinátájú pontja, amelyről biztosan tudjuk, hogy része lesz $P$ konvex burkának), és keresünk hozzá egy olyan $p_{i+1}=f(p_{i},P)$ pontot, hogy a $P$ halmaz összes többi pontja a $p_{i}p_{i+1}$ egyenestől jobbra legyen. Itt a $p_{i+1}=f(p_{i},P)$ jelölés azt jelenti, hogy a következő pontot ($p_{i+1}$-et) $p_{i}$ és $P$ függvényében határozzuk meg. A $Q_{k}$ részhalmaz $C_{k}$ konvex burka ismert, és maximum $m$ pontot tartalmaz (az óramutató járásával megegyező, vagy ellentétes irányban felsorolva), így $f(p_{i},Q_{k})$ bináris kereséssel kiszámítható $O(\log m)$ idő alatt. Tehát $O(K\log m)$ idő alatt a $K$ darab részhalmaz mindegyikére kiszámítható az $f(p_{i},Q_{k})$. Ezek után $f(p_{i},P)$ is meghatározható a szimpla Jarvis-féle meneteléssel, viszont elég csak az $(f(p_{i},Q_{k}))_{1\leq k\leq K}$ pontokat, vagyis a kis konvex burkok pontjait figyelembe venni a teljes $P$ halmaz pontjai helyett. Azon pontok felhasználásával pedig egy újabb pont megtalálásához a Jarvis-féle menetelés futási ideje $O(K)$, ami elhanyagolható az $f(p_{i},Q_{k})$-k kiszámításához képest. A Jarvis-féle menetelés akkor fejeződik be, ha $O(h)$ alkalommal megismétlődött (mivel a lényege, hogy maximum $h$ ismétlés után mindenképp megtaláljuk a $P$ halmaz konvex burkát, ahol $h$ a konvex burok pontjainak száma), tehát a második fázis $O(Kh\log m)$ időt fog igénybe venni, ami egyenlő $O(n\log h)$-val, ha $m$ egy $h$-hoz közeli érték (lásd lejjebb $m$ megválasztásának stratégiáját).

A két fázis összesen $O(n\log h)$ idő alatt számítja ki az $n$ pont konvex burkát.

Az $m$ paraméter megválasztása

Ha $m$ szabadon választható paraméter, akkor előfordulhat, hogy $m<h$. Ebben az esetben a második fázisban $m$ lépés után leállítjuk a Jarvis-féle mentelést, hogy ne legyen túl nagy a futásidő, és $O(n\log m)$ idő elteltével a konvex burok még nem lesz kiszámítva.

Ezért azt az ötletet alkalmazzuk, hogy többször is lefuttatjuk az algoritmust egyre nagyobb $m$ értékkel. A futás minden $m$-re $O(n\log m)$ idő alatt befejeződik (eredményesen vagy eredménytelenül). Ha $m$ túl lassan növekszik, akkor nagy lehet a szükséges iterációk száma, ellenben ha túl gyorsan, akkor az első $m$, amire sikeresen lefut, sokkal nagyobb lehet, mint $h$, így lassabbá válhat a futásidő: $O(n\log m)>O(n\log h)$.

Négyzetre emelős stratégia

Egy lehetséges stratégia, hogy minden iterációnál négyzetre emeljük $m$ értékét, maximum $n$-ig. $m=2$-vel kezdve, a $t.$ iterációnál $m=\min \left(n,2^{2^{t}}\right)$ legyen. Ebben az esetben $O(\log \log h)$ iteráció lesz, mivel az algoritmus befejeződik, amint

$m=2^{2^{t}}\geq h\iff \log \left(2^{2^{t}}\right)\geq \log h\iff 2^{t}\geq \log h\iff \log {2^{t}}\geq \log {\log h}\iff t\geq \log {\log h},$

ahol 2-es alapú logaritmust veszünk, és az algoritmus teljes futásideje

$\sum _{t=1}^{\lceil \log \log h\rceil }O\left(n\log \left(2^{2^{t}}\right)\right)=O(n)\sum _{t=1}^{\lceil \log \log h\rceil }O(2^{t})=O\left(n\cdot 2^{1+\lceil \log \log h\rceil }\right)=O(n\log h).$

Háromdimenziós térben

Ha háromdimenziós esetre akarjuk általánosítani, akkor a Graham-féle pásztázás helyett egy $O(n\log n)$ algoritmust kell használnunk a háromdimenziós konvex burok kiszámítására, illetve a Jarvis-féle menetelés háromdimenziós változatát. A futásidő marad $O(n\log h)$.

Fordítás

Ez a szócikk részben vagy egészben a Chan's algorithm című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.