Monty Hall-paradoxon

A Monty Hall-paradoxon egy valószínűségi paradoxon, ami az Amerikai Egyesült Államokban futott Let's Make a Deal (Kössünk üzletet) című televíziós vetélkedő utolsó feladatán alapul, nevét a vetélkedő műsorvezetőjéről, Monty Hallról kapta. (A műsor magyar változatának címe Zsákbamacska volt, és Rózsa György vezette.)

Az autót keresvén a 3. ajtót választjuk, erre Monty megmutatja, hogy az 1. ajtó mögött kecske van, és megkérdi, akarunk-e váltani. Jobbak az esélyeink, ha váltunk.

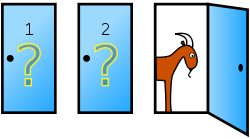
A műsor végén a játékosnak mutatnak három csukott ajtót, amelyek közül kettő mögött egy-egy kecske van, a harmadik mögött viszont egy vadonatúj autó. A játékos nyereménye az, ami az általa kiválasztott ajtó mögött van. Azonban a választás meg van egy kicsit bonyolítva. Először a játékos csak rámutat az egyik ajtóra, de mielőtt valóban kinyitná, a műsorvezető a másik két ajtó közül kinyit egyet, amelyik mögött nem az autó van (a játékvezető tudja, melyik ajtó mögött mi van), majd megkérdezi a játékost, hogy akar-e módosítani a választásán. A játékos ezután vagy változtat, vagy nem, végül kinyílik az így kiválasztott ajtó, mögötte a nyereménnyel. A paradoxon nagy kérdése az, hogy érdemes-e változtatni, illetve hogy számít-e ez egyáltalán.

Egyszerű valószínűségszámítási eszközökkel megmutatható, hogy igen, mindig érdemes váltani, ez azonban annyira ellentmond a józan észnek, hogy a problémát paradoxonnak tekinthetjük.

A probléma és megoldása

Az autót keresvén az 1. ajtót választjuk, erre Monty megmutatja, hogy a 3. ajtó mögött kecske van, és megkérdi, akarunk-e váltani. Jobbak az esélyeink, ha váltunk.

A probléma

Az alábbi idézet Craig F. Whitaker Marylin vos Savanthoz, a Parade magazin rovatvezetőjéhez írt levele egy részletének fordítása, 1990-ből:

Képzeljük el, hogy egy vetélkedőben szerepel, és három ajtó közül kell választania. Az egyik mögött kocsi van, a másik kettő mögött viszont kecske. Tegyük fel, hogy maga az 1. ajtót választja, mire a műsorvezető, aki tudja, melyik ajtó mögött mi van, kinyitja a 3. ajtót, megmutatván, hogy amögött kecske van. Ezután önhöz fordul, és megkérdezi: „Nem akarja esetleg mégis a 2. ajtót választani?” Vajon előnyére válik, ha vált?

Ez a feladat eredeti, Steve Selvin által kitalált változatának egy átfogalmazása. Selvin 1975 februárjában írta le a problémát egy az American Statistician című lapnak írt levelében. Az eredeti vetélkedőben a játékosoknak valójában nem volt lehetőségük váltásra, ha már egyszer eldöntötték, hogy melyik ajtót választják, ahogy Monty Hall írta Selvinnek az eredeti problémafelvetésre válaszul:

És ha valamikor bejut a műsoromba, a szabályok magára is vonatkozni fognak – ha egyszer választott, már nincs változtatás.

Selvin ezt követő levele az American Statistician-nek 1975 augusztusában elsőként hivatkozott a problémára Monty Hall-paradoxon néven.

Az ezzel majdnem pontosan egyező, „három börtönlakó” problémát már 1959-ben publikálta Martin Gardner. Gardner leírása pontosabb, mert ezzel a változattal ellentétben nála nincsenek ki nem mondott feltételezések.

A „józan ész”

A józan ész logikája a legtöbb embernek azt diktálja, hogy mindegy, váltok-e vagy sem. Az érvelés a következő: ha két ajtó van csukva, az egyik mögött autó, a másik mögött kecske, akkor 50-50% az esélye, hogy az autót nyerem, akármelyiket is választom. Látszólag az, hogy a korábbi döntést figyelmen kívül hagyva, „tiszta lappal kezdve” választok egy ajtót, vagy hogy az előző választásomat módosíthatom, nem befolyásol semmit.

A megoldás

A helyes válasz az igen, az esélyeink az autó megnyerésére megduplázódnak, ha váltunk. Amikor a játékos először kiválaszt egy ajtót, 1/3 az esélye, hogy az autót választotta, 2/3 az esélye, hogy kecskét. Az, hogy a műsorvezető ezek után kinyitja a másik két ajtó egyikét, megmutatván egy kecskét, nem változtat ezeken a valószínűségeken, továbbra is 1/3 az esélye, hogy az elsőre választott ajtó mögött van az autó. Csakhogy ezen a ponton a két másik ajtó közül már csak az egyik van csukva – annak a valószínűsége pedig, hogy az autó valamelyik csukott ajtó mögött van, még mindig 100% –, ezért tehát 2/3 valószínűséggel a másik csukott ajtó mögött van a kocsi.

Még egyszer, kicsit átfogalmazva: csak az esetek egyharmadában választhatja Monty a fennmaradó ajtók bármelyikét kinyitásra (mivelhogy mi elsőre az autót választottuk), az esetek kétharmadában kénytelen egy bizonyos ajtót választani (mert egy kecskét mi foglalunk, az autót pedig nem választhatja).

Segítség a magyarázat megértéséhez

• Az alábbi példában a játékos a 3. ajtót választotta először.

• Könnyebben átláthatunk a szitán, ha három ajtó helyett százat képzelünk el. Továbbra is egy mögött van autó, de most 99 mögött van kecske. Az első választáskor 100 esetből 99-szer kecskét választunk, és csak 1-szer autót. Ha ezután Monty 98 kecskét rejtő ajtót kinyit, 100 esetből 99-szer az egyetlen másik csukva hagyott mögött van az autó, és csak 1 esetben van mögötte kecske. Nyilvánvaló tehát, hogy érdemes váltani.
• Egy másik lehetséges megfogalmazás: ha a játékos eredetileg kecskét választott, akkor biztos megmutatják neki a másik kecskét, így a váltással biztosítja, hogy nyerjen. Mivel eredetileg 2/3 esélye van kecskét választani, a váltással 2/3 eséllyel nyer.
• Ahelyett, hogy Monty kinyit egy kecskét rejtő ajtót, az is működik, ha a két, játékos által nem választott ajtót „összevonjuk”. Így tkp. a játékos azt dönti el, hogy megmarad az eredetileg választott egyetlen ajtónál, vagy inkább vált, és mind a két másik ajtót kinyitja. Az pedig nyilvánvaló, hogy két ajtó kinyitásával jobbak az esélyeink az autót megnyerni, mint eggyel.
• Megpróbálhatjuk sokszor képzeletben (vagy valaki segítségével ténylegesen) lejátszani a játékot. Első körben soha ne cseréljünk. Hamar észre fogjuk venni, hogy teljesen mindegy, melyik ajtót nyitja ki a műsorvezető, csak akkor fogunk nyerni, ha már elsőre is jól választottunk, azaz 1/3 eséllyel. Második nekifutásra mindig cseréljünk! A cserével csak akkor nyerünk, ha elsőre nem az autót választottuk ki (átlagosan 3 esetből 2-szer), ennek a valószínűsége pedig 2/3.
• Az is egy lehetőség, hogy a játékos a véletlenre bízza döntést. Az első választás eredményét is a véletlen határozta meg, akkor maradjunk ennél. Feldob egy érmét, ha fej akkor marad, ha írás akkor vált. Az eredmény 50% nyerési esély. Ez jobb mintha maradna, rosszabb mintha váltana. Egy előnye van lélektani szempontból, az eredmény megfelel a megérzésnek.
• Az is egy lehetőség, hogy felírjuk az összes esetet. Tegyük fel, hogy a játékos mindig az 1. ajtót választja. (Az esetek szimmetrikusak abból a szempontból, hogy melyik ajtót választjuk, pontosan ugyanez a három lehetőség lenne, ha a 2. vagy a 3. ajtót választanánk.)

1. ajtó	2. ajtó	3. ajtó	Monty kinyitja	Ha váltunk
kecske	kecske	autó	a 2. ajtót	nyerünk
kecske	autó	kecske	a 3. ajtót	nyerünk
autó	kecske	kecske	a 2. vagy a 3. ajtót	vesztünk

A három esetből kétszer nyertünk, ha váltottunk.

Különbséget kell tenni az autó elhelyezkedésének valószínűsége és az autó megtalálásának valószínűsége között. A fenti magyarázatok csak az autó elhelyezkedésének valószínűségét veszik figyelembe. Két zárt ajtónál (a már kinyitott ajtóban kecske) a megtalálás valószínűsége 1/2.

Változatok

Két játékos

Ebben a változatban ugyanúgy három ajtó van, egy autó, két kecske, de ezúttal két játékos választ egy-egy ajtót. (Nem ugyanazt.) A következő lépésben az egyik játékos, aki kecskét választott, kiesik, Monty pedig kinyitja az általa választott ajtót, majd felteszi a bent maradó játékosnak a szokásos kérdést. Ha mindkét játékos kecskét választott, Monty véletlenszerűen dönti el, hogy ki fejezi be a játékot. (Természetesen erről a játékosok nem tudnak.) A kérdés ezután ugyanaz: érdemes-e a bennmaradt játékosnak váltania?

A fenti táblázatos formához hasonlóan itt is fel lehet írni az eseteket. Tegyük fel, hogy az 1. játékos mindig az 1. ajtót, a 2. játékos mindig a 2. ajtót választja.

1. ajtó	2. ajtó	3. ajtó	kiesik	váltás
kecske	kecske	autó	valamelyik	nyer
kecske	autó	kecske	1. játékos	veszít
autó	kecske	kecske	2. játékos	veszít

A három esetből kétszer veszítünk, ha váltanánk. Viszont a középső esetben (a másik játékos választja az autót) a játék számunkra véget ér akkor, amikor Monty a mi ajtónkat nyitja ki és a másik játékos folytathatja (ekkor tehát el sem jutunk addig, hogy Monty felkínálja a váltást). Ugyanígy véget ér a játék 50% eséllyel akkor is, ha mind a két játékos kecskés ajtóra fogadott (és Monty minket választott). A ajtóváltás utáni lehetséges kimenetelek vizsgálatakor tehát csak az első és a harmadik esetet kell vizsgálnunk, amikből az egyik esetben nyerünk, a másikban veszítünk, tehát pontosan akkora eséllyel nyerjük meg az autót akkor is, ha ajtót váltunk mintha nem.

N ajtó

Tegyük fel, hogy most n ajtónk van. Az első lépésben kiválasztunk egyet, Monty pedig megmutat egy másikat, amelyik mögött kecske van. Ezután ha akarunk, válthatunk, vagy maradhatunk ugyanott. Monty ezután újabb ajtót nyit ki, majd ismét válthatunk, és így tovább, amíg végül már csak két csukott ajtó van, az, amelyiket legutóbb választottuk, és még egy. A kérdés, hogy milyen váltási stratégiát érdemes követni, hányszor és mikor érdemes váltani?

A válasz: maradjunk az első döntésünknél egészen a végéig, amikor már csak két ajtó van, és akkor váltsunk, ilyenkor a nyerés valószínűsége (n-1)/n. Bapeswara Rao és Bhaskara Rao bizonyította, hogy ez a legjobb stratégia.

Hivatkozások

• Egy egyszerű PHP program a paradoxon demonstrálására Archiválva 2012. szeptember 27-i dátummal a Wayback Machine-ben

Irodalomjegyzék

• Rao, V. V. Bapeswara and Rao, M. Bhaskara, "A Three Door Game Show and Some of its Variants," Mathematical Scientist, vol. 17, pp. 89–94, 1992.
• Bohl, Alan H.; Liberatore, Matthew J.; and Nudick, Robert L. (1995). "A Tale of Two Goats … and a Car, or The Importance of Assumptions in Problem Solutions". Journal of Recreational Mathematics 1995, pp. 1–9.
• Gardner, Martin (1959). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182.
• Selvin, Steve (1975a). "A problem in probability" (letter to the editor). American Statistician 29(1):67 (February 1975).
• Selvin, Steve (1975b). "On the Monty Hall problem" (letter to the editor). American Statistician 29(3):134 (August 1975).
• Tierney, John (1991). "Behind Monty Hall's Doors: Puzzle, Debate and Answer?", The New York Times July 21, 1991, Sunday, Section 1; Part 1; Page 1; Column 5
• vos Savant, Marilyn (1990). "Ask Marilyn" column, Parade Magazine p. 12 (Feb. 17, 1990). [cited in Bohl et al., 1995]