Csillagszínezés

A matematika, azon belül a gráfelmélet területén egy G gráf csillagszínezése (star coloring) olyan csúcsszínezés, amiben bármely négy csúcson átmenő út legalább 3 különböző színt tartalmaz. Ezzel egyenértékű megfogalmazásban, a csillagszínezésben bármely két szín által meghatározott feszített részgráfok összefüggő komponensei csillaggráfok. A csillagszínezést (Grünbaum 1973) vezette be.

A Dyck-gráf csillagkromatikus száma 4, míg kromatikus száma 2.

Csillagkromatikus szám

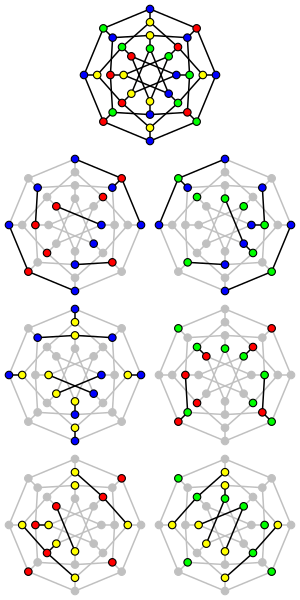
A $\chi _{s}(G)$ csillagkromatikus szám a G csillagszínezéséhez szükséges legkevesebb szín száma.

A csillagszínezés egyik általánosítása az aciklikus (körmentes) színezés; itt minden körnek legalább három színt kell használnia, ezért a két szín által meghatározott feszített részgráfok erdők. Ha a G gráf aciklikus kromatikus számát $\chi _{a}(G)$-vel jelöljük, $\chi _{a}(G)\leq \chi _{s}(G)$, és valójában minden csillagszínezés egyben aciklikus színezés is.

A csillagkromatikus szám (Nešetřil & Ossona de Mendez 2003) alapján minden minorra zárt gráfosztályon korlátos. Ezt az eredményt (Nešetřil & Ossona de Mendez 2006) tovább általánosította az összes alacsony fa-mélységű színezésre (a normál színezés és a csillagszínezés olyan alacsony fa-mélységű színezésnek tekinthető, melyek megfelelő paramétere 1, illetve 2).

További eredmények:

${\text{Ha }}\chi _{a}(G)\leq k,{\text{ akkor }}\chi _{s}(G)\leq k\cdot 2^{k-1}$

A fentiből következik, hogy ha G síkgráf, akkor $\chi _{s}(G)\leq 80$

$\chi _{s}(G)\leq \chi _{a}(G)(2\chi _{a}(G)-1)$

A fentiből következik, hogy ha G síkgráf, akkor $\chi _{s}(G)\leq 45$

A fentiből szintén következik, hogy ha a G síkgráf girthparamétere g, akkor:

${\begin{cases}\;{\mbox{ha }}g\geq 7{\text{, akkor }}\chi _{s}(G)\leq 9,\\\;{\text{ha }}g\geq 5{\text{, akkor }}\chi _{s}(G)\leq 16.\end{cases}}$

Ha G síkgráf, akkor $\chi _{s}(G)\leq 30$

Ha G síkgráf, akkor $\chi _{s}(G)\leq 20$

Ha a G gráf favastagsága legfeljebb k, akkor $\chi _{s}(G)\leq k(k+3)/2+1$

Ennek következménye: ha G külsíkgráf, akkor $\chi _{s}(G)\leq 6$ és ez az eredmény éles.

Sejtés: létezik olyan G síkgráf, melyre $\chi _{s}(G)=10$

Számítási bonyolultság

(Coleman & Moré 1984) megmutatták, hogy az optimális csillagszínezés megtalálása NP-teljes még akkor is, ha G páros gráf.

(Albertson et al. 2004) megmutatták, hogy annak eldöntése, hogy $\chi _{s}(G)\leq 3$ NP-teljes, még akkor is, ha G-ről ismert, hogy síkgráf és páros.

Jegyzetek

• Albertson, Michael O.; Chappell, Glenn G. & Kierstead, Hal A. et al. (2004), "Coloring with no 2-Colored P₄'s", The Electronic Journal of Combinatorics 11 (1), <http://www.combinatorics.org/Volume_11/Abstracts/v11i1r26.html>.
• Coleman, Thomas F. & Moré, Jorge (1984), "Estimation of sparse Hessian matrices and graph coloring problems", Mathematical Programming 28 (3): 243–270, DOI 10.1007/BF02612334.
• Fertin, Guillaume; Raspaud, André & Reed, Bruce (2004), "Star coloring of graphs", Journal of Graph Theory 47 (3): 163–182, DOI 10.1002/jgt.20029.
• Grünbaum, Branko (1973), "Acyclic colorings of planar graphs", Israel Journal of Mathematics 14: 390–408, DOI 10.1007/BF02764716.
• Nešetřil, Jaroslav & Ossona de Mendez, Patrice (2003), "Colorings and homomorphisms of minor closed classes", Discrete & Computational Geometry: The Goodman-Pollack Festschrift, vol. 25, Algorithms & Combinatorics, Springer-Verlag, pp. 651–664.
• Nešetřil, Jaroslav & Ossona de Mendez, Patrice (2006), "Tree depth, subgraph coloring and homomorphism bounds", European Journal of Combinatorics 27 (6): 1022–1041, DOI 10.1016/j.ejc.2005.01.010.

További információk

• Star colorings and acyclic colorings (1973), present at the Research Experiences for Graduate Students (REGS) at the University of Illinois, 2008.
• André Raspaud: Star Coloring of Graphs (2009)