Dubins-út
A matematika, azon belül a geometria területén a Dubins-út (Dubins path) alatt az két pontot a kétdimenziós euklideszi síkban összekötő olyan, legrövidebb görbét értünk, ahol az út görbületére megszorítással élünk, előírjuk az út kezdeti és befejező iránytangenseit, és feltételezzük, hogy az út mentén haladó jármű csak előre képes haladni. Ha a jármű tolatásra is képes, az út a Reeds–Shepp-görbét követi.[1]
1957-ben Lester Eli Dubins (1920–2010)[2] geometriai érvelés segítségével megmutatta,[3] hogy egy ilyen útvonal mindig maximális görbületű és/vagy egyenes szakaszokból áll össze. Más megfogalmazásban, a legrövidebb út maximális görbületű, illetve egyenes szakaszok összeillesztésével állítható elő. Ugyanezt később a Pontrjagin-féle maximumelv felhasználásával is sikerült igazolni.[4]
A robotika és az irányításelmélet a Dubins-utat a guruló robotok, repülőgépek és víz alatti járművek útvonalainak tervezésére használja. Egyszerű mértani[5] és analitikus módszerek[6] segítségével lehet az optimális útvonalat kiszámítani.
Például egy kerékkel ellátott robotra alkalmazható egyszerű kinematikus gépkocsi-modell:
ahol a jármű helyzete, a mozgásirány, a jármű konstans sebességgel mozog, az fordulékonyság pedig korlátozott. Ebben az esetben a maximális fordulási ráta valamely minimális fordulási sugárnak felel meg (és ezzel egyenértékű módon a maximális görbületnek). A Dublins-út két irányított pont közötti legrövidebb útvonalat határozza meg, ami egy kerekekkel ellátott robot számára megfelelő.
Az optimális útvonal leírható a gépkocsi-analógia segítségével, a „jobbkanyar (R)”, „balkanyar (L)” és az „egyenes irányban való hajtás (S)” opciókkal. Egy optimális útvonal a hat alaptípus valamelyikét tartalmazni fogja: RSR, RSL, LSR, LSL, RLR, LRL. Tehát ha valamely kezdeti pozícióhoz, befejező pozícióhoz és irányhoz egy „RSR” típusú útvonal tartozik, akkor kezdetben egy jobbra kanyarodást (R) kell végezni, majd egyenes vonalú mozgást (S), végül egy újabb jobbkanyart (R). A lépéssor minden elemét a megfelelő hosszúságban kibontva a legrövidebb utat kapjuk az A és a B pont között a kívánt iránytangensekkel, a megadott görbületet meg nem haladva.
-
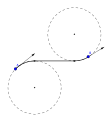
Egy RSL Dubins-út
-
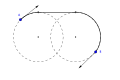
Egy RSR Dubins-út
-
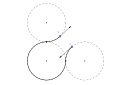
Egy LRL Dubins-út
Jegyzetek
szerkesztés- ↑ Reeds, J.A. and L.A. Shepp, "Optimal paths for a car that goes both forwards and backwards" Archiválva 2017. január 19-i dátummal a Wayback Machine-ben, Pacific J. Math., 145 (1990), pp. 367–393.
- ↑ IN MEMORIAM Lester Eli Dubins Professor of Mathematics and Statistics, Emeritus UC Berkeley 1920–2010. University of California. [2011. szeptember 15-i dátummal az eredetiből archiválva]. (Hozzáférés: 2012. május 26.)
- ↑ Dubins, L.E. (1957. július 1.). „On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents”. American Journal of Mathematics 79 (3), 497–516. o. DOI:10.2307/2372560.
- ↑ Boissonat, J.D. (1992. május 1.). „Shortest Paths of Bounded Curvature in the Plane”. Proceedings of the IEEE International Conference on Robotics and Automation 3: 2315–2320. doi:10.1109/ROBOT.1992.220117.
- ↑ Anisi, David (2003. július 1.). „Optimal Motion Control of a Ground Vehicle”, Kiadó: Swedish Research Defence Agency. I650-1942.
- ↑ Bui, X.N. (1994. május 1.). „Shortest Path Synthesis for Dubins Non-Holonomic Robot”. IEEE Conference on Robotics and Automation 1: 2–7. doi:10.1109/ROBOT.1994.351019.
További információk
szerkesztés- Dubins Curves Archiválva 2016. március 22-i dátummal a Wayback Machine-ben, from Planning Algorithms by Steven M. LaValle
- A Comprehensive, Step-by-Step Tutorial to Computing Dubin’s Paths