O jelölés

Az Edmund Landautól származó ordó-jelölés (O jelölés) az analízisben és alkalmazásaiban (valószínűségszámítás, analitikus számelmélet, számításelmélet) függvények becslését megkönnyítő jelölésmód.

Egy példa az ordó-jelölés használatára: f(x) ∈ O(g(x)) vagyis létezik egy c > 0 és létezik egy x₀ úgy, hogy f(x) < cg(x), ha x > x₀.

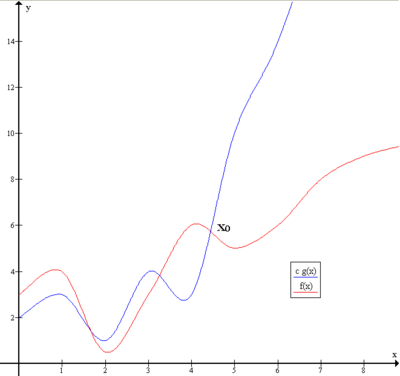
Nagy ordó

Ha $f$ és $g$ valós vagy természetes számokon értelmezett függvények, amelyeknek nagy x helyeken felvett értékeit, vagy éppen $x\in [a,b]$ (a,b valós számok) melletti viselkedését vizsgáljuk, akkor $f(x)=O(g(x))$ azt jelenti, hogy $|f(x)|\leq Cg(x)$ teljesül alkalmas C valós konstansra a megadott helyen. Kiejtése: „$f(x)$ egyenlő (nagy) ordó $g(x)$”. Ezt leggyakrabban hibatagok menet közbeni becslésére alkalmazzuk, például $(x+1)^{2}=x^{2}+O(x)$ $x\to \infty$ mellett, hiszen a hibatag $2x+1$, legfeljebb 3x minden $x\geq 1$-re. Hasonlóképpen írható például $e^{x}=1+x+O(x^{2})$, ahol $x\to 0$.

Tulajdonságok

Ha egy f függvény felírható mint véges sok függvény összege, akkor a növekedési ütemet a leggyorsabban növekvő határozza meg. Például:

$f(n)=9\log n+5(\log n)^{3}+3n^{2}+2n^{3}=O(n^{3})\,,\qquad {\text{ahogy }}n\to \infty \,\!.$

Szorzat

$f_{1}\in O(g_{1}){\text{ és }}f_{2}\in O(g_{2})\,\Rightarrow f_{1}f_{2}\in O(g_{1}g_{2})\,$

$f\cdot O(g)\subset O(fg)$

Összeg

$f_{1}\in O(g_{1}){\text{ és }}f_{2}\in O(g_{2})\,\Rightarrow f_{1}+f_{2}\in O(|g_{1}|+|g_{2}|)\,$

Ami azt jelenti, hogy $f_{1}\in O(g){\text{ and }}f_{2}\in O(g)\Rightarrow f_{1}+f_{2}\in O(g)$.

Ha f és g pozitív függvények, akkor $f+O(g)\in O(f+g)$

Konstanssal való szorzás

Legyen k egy konstans. Ekkor:

$\ O(kg)=O(g)$ ha k nem nulla.

$f\in O(g)\Rightarrow kf\in O(g).$

Kapcsolódó jelölések

Kis ordó

Ha nemcsak $|f(x)|\leq Cg(x)$, de $f(x)/g(x)\to 0$ is teljesül a megadott határátmenetben, azt $f(x)=o(g(x))$-szel jelöljük és azt mondjuk, hogy „$f(x)$ egyenlő kis ordó $g(x)$”. Eszerint például $x^{2}=o(x^{3})$ $x\to \infty$ mellett, vagy $\log n!=(1+o(1))n\log n$ szintén $n\to \infty$ esetén.

Omega

Ha nem felülről, hanem alulról adunk becslést, azt omegával jelöljük. Eszerint $f(x)=\Omega (g(x))$ azt jelenti, hogy a megadott helyeken $f(x)>cg(x)$ teljesül alkalmas $c>0$ konstansra.

Theta

Ha az $f,g$ függvényekre $f(x)=O(g(x))$ és $g(x)=\Omega (f(x))$ is teljesül, azt $f(x)=\theta (g(x))$-szel jelöljük. Így például Csebisev tétele a prímszámok számáról így fogalmazható:

$\pi (x)=\theta \left({\frac {x}{\log x}}\right).$

A theta-jelölés helyett használják az $f(x)\asymp g(x)$ jelölést is.

Vinogradov-szimbólum

Vinogradov vezette be $f(x)\ll g(x)$-t $f(x)=O(g(x))$ jelölésére.

Fordítás

Ez a szócikk részben vagy egészben a Big O notation című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.