Élösszehúzás
A gráfelmélet területén az élösszehúzás (edge contraction) olyan gráfművelet, ami a gráf egy élét eltávolítja, miközben az él által korábban összekötött két csúcsot összeolvasztja. Az élösszehúzás a gráfminorok elméletének alapvető művelete. A csúcsazonosítás a művelet kevésbé korlátozott formája.
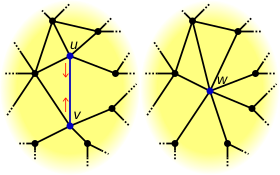
Definíció
szerkesztésAz élösszehúzás művelet a gráf egy adott e élén hajtható végre. Az e él eltávolításra került, a két szomszédos csúcs, u és v pedig összevonódik egy új w csúcsba, ahol a w-be menő élek pontosan azok lesznek, melyek akár u, akár v csúcsba mentek korábban. Általánosabban értelmezhető az élösszehúzás élek egy halmazára is (ilyenkor az élek egyenként, tetszőleges sorrendben összehúzhatók, a végeredmény ugyanaz lesz).[1]
A lentebb definiált élösszehúzás-művelet többszörös éleket eredményezhet akkor is, ha a kiindulási gráf egyszerű volt. Sőt hurokélek is keletkezhetnek. Egyes szerzők azonban[2] nem engedik meg a többszörös élek létrejöttét, így az általuk definiált élösszehúzás egyszerű gráfokon mindig egyszerű gráfokhoz vezet.
Formális definíció
szerkesztésTekintsünk egy G=(V,E) gráfot (vagy irányított gráfot), mely tartalmaz egy e=(u,v) élet, ahol u≠v. Legyen f függvény az a függvény, ami V\{u,v} minden csúcsát magába viszi át, a maradékot pedig az új w csúcsba. Az e összehúzása az új G′=(V′,E′) gráfot eredményezi, ahol V′=(V\{u,v})∪{w}, E′=E\{e}, és minden x∈V, x′=f(x)∈V′ pontosan akkor szomszédos az e′∈E′ éllel, ha a megfelelő, G gráfbeli e∈E él szomszédos x-szel.
Csúcsazonosítás
szerkesztésA csúcsazonosítás (néha csúcsösszehúzás) megszünteti azt a korlátozást, hogy az „összehúzásnak” egy éllel összekötött két csúcs között kell végbemennie. (Tehát az élösszehúzás a csúcsazonosítás speciális esete.) Ez a művelet a gráf bármely csúcspárján (vagy csúcshalmazán) végrehajtható. Az összehúzandó csúcsok közötti éleket egyes értelmezések szerint el kell távolítani. Ha v és v' G különböző komponenseibe tartozó csúcsok, akkor a G' gráf létrehozható a v és v' csúcsok azonosításával egy új G'-beli v csúccsá.[3]
Csúcshasítás
szerkesztésA csúcshasítás vagy csúcsszétvágás azt jelenti, hogy egy v csúcsot helyettesítünk a szomszédos v′ és v′′ csúcsokkal, az e = vu éleket pedig vagy a v′u, vagy a v′′u fogja helyettesíteni, tehát ha az eredeti csúcs szomszédos volt a gráf egy csúcsával, akkor a két új csúcs közül legalább az egyik szomszédos lesz vele. A G' gráfbeli v′v′′ él a hasító él. A csúcsazonosítás fordított művelete.[4]
Útösszehúzás
szerkesztésAz útösszehúzás során egy út összes éleit húzzuk össze egyetlen, az út végpontjai közötti éllé. Az út menti csúcsokkal szomszédos éleket vagy megszüntetjük, vagy véletlenszerűen, vagy szisztematikusan az egyik végponthoz csatoljuk őket.
Alkalmazásai
szerkesztésAz élösszehúzási és csúcsazonosítási technikák gyakran jönnek elő a gráf csúcsainak vagy éleinek számával kapcsolatos teljes indukciós bizonyításokban, ahol egy tulajdonság teljesül kisebb gráfokra, és ennek a felhasználásával igazolják, hogy nagyobb gráfokra is teljesül.
Az élösszehúzás szerepel a tetszőleges összefüggő gráf feszítőfái számát meghatározó rekurzív képletben is,[1] valamint az egyszerű gráf kromatikus polinomját meghatározó rekurzív képletben is.[5]
Az összehúzási műveletek hasznosak lehetnek, ha egy gráfot oly módon szeretnénk leegyszerűsíteni, hogy a lényegében ekvivalens entitásokat megjelenítő csúcsokat azonossá tesszük. A leggyakoribb példa erre az általános irányított gráf körmentes irányított gráffá alakítása erősen összefüggő komponensek csúcsainak azonosítása. Ha a gráf által leírt reláció tranzitív, nem történik információvesztés, amennyiben az egyesített csúcsok maradéktalanul megkapják a kitörölt csúcsok címkéit.
Egy másik példa a gráfszínezés-alapú regiszterallokáció során a regiszterek összeolvasztása; itt a csúcsok, ha biztonságosan összehúzhatók, akkor csökken a különböző változók közötti felesleges mozgatási műveletek száma.
Az élösszehúzás megjelenik különböző 3D modellezési szoftvercsomagokban, itt a fő cél a gyorsabb kalkulációt lehetővé tevő, alacsony sokszögszámú konzisztens modellek elkészítése.
Kapcsolódó szócikkek
szerkesztésJegyzetek
szerkesztés- ↑ a b Gross & Yellen 1998, p. 264
- ↑ Rosen 2011, p. 664
- ↑ Oxley 1992, pp. 147-148
- ↑ Vertex Splitting and Upper Embeddable Graphs
- ↑ West 2001, p. 221
- Gross, Jonathan & Yellen, Jay (1998), Graph Theory and its applications, CRC Press, ISBN 0-8493-3982-0
- Oxley, James (1992), Matroid Theory, Oxford University Press
- Rosen, Kenneth (2011), Discrete Mathematics and Its Applications (7th ed.), McGraw-Hill, ISBN 9780073383095
- West, Douglas B. (2001), Introduction to Graph Theory (2nd ed.), Prentice-Hall, ISBN 0-13-014400-2
További információk
szerkesztés- Weisstein, Eric W.: Edge Contraction (angol nyelven). Wolfram MathWorld