Monte Carlo-módszer
A Monte Carlo-módszer egy olyan sztochasztikus szimulációs módszer, amely számítástechnikai eszközök segítségével előállítja egy adott kísérlet végeredményét, ezek után az eredményként kapott numerikus jellemzőket feljegyzik és kiértékelik. Az eredmény hibájának meghatározása szórás kiszámításával történik. Az álvéletlen számokat, melyek a kísérletekben szereplő valószínűségi változók értékei, számítógép állítja elő. Több programnyelv is tartalmaz ilyen álvéletlenszám-generátort, pl. a C programnyelv. Hasonló véletlen számokat lehetne generálni a kaszinók kedvelt játékával, a rulettel is. A módszert Nicolas Metropolis (Teller Ede közreműködésével) fejlesztette ki Los Alamosban a sűrű folyadékok szimulációjára,[1] és segítségével Enrico Fermi, Stan Ulman és Neumann János - ők ketten javasolták a Monte Carlo elnevezést - szinte azonnal elvégezte a nem harmonikus, egy dimenziós kristályok nagyon híres numerikus tanulmányozását.[2] Felhasználási területe mára már majdnem minden természettudományos diszciplínára kiterjedt. Alkalmazták a társadalomtudományokban is, például a szociológiában, a pszichológiában és a politikatudományban
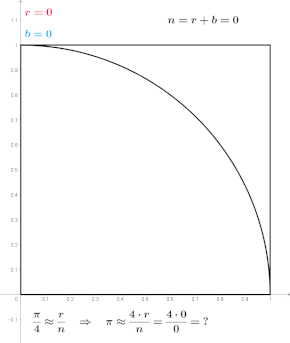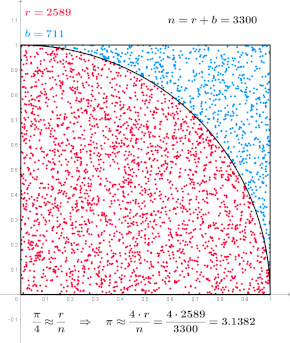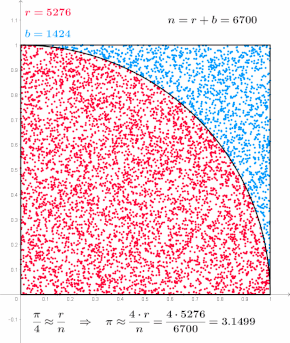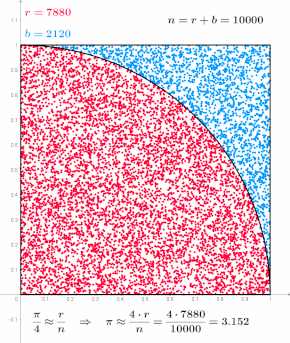
A Monte Carlo-módszereket főként három különálló problémaosztályban használják: optimalizálás, numerikus integráció és rajzok generálása valószínűségi eloszlásból. Használhatók olyan jelenségek modellezésére is, amelyek bemenetei jelentős bizonytalansággal járnak, mint például az atomerőmű meghibásodásának kockázatának kiszámítása. A Monte Carlo-módszereket gyakran számítógépes szimulációkkal valósítják meg, és közelítő megoldásokat tudnak adni olyan problémákra, amelyek egyébként megoldhatatlanok vagy túl bonyolultak ahhoz, hogy matematikailag elemezzék őket.
A Monte Carl-módszereknek is vannak korlátai és kihívásai, mint például a pontosság és a számítási költségek közötti kompromisszum, a dimenzionalitás átka, a véletlenszám-generátorok megbízhatósága, valamint az eredmények ellenőrzése és validálása.
Források
szerkesztés- Bevezetés (angol)
- MIAU wiki Archiválva 2013. március 25-i dátummal a Wayback Machine-ben
- MathWorld
- Café Math
- Feynman-Kac models and interacting particle systems
Jegyzetek
szerkesztés
|
Ez a fizikai témájú lap egyelőre csonk (erősen hiányos). Segíts te is, hogy igazi szócikk lehessen belőle! |
|
Ez az informatikai tárgyú lap egyelőre csonk (erősen hiányos). Segíts te is, hogy igazi szócikk lehessen belőle! |
|
Ez a matematikai tárgyú lap egyelőre csonk (erősen hiányos). Segíts te is, hogy igazi szócikk lehessen belőle! |
