Wikipédia

Hipohamiltoni gráf

olyan gráf, mely nem rendelkezik Hamilton-körrel, de tetszőleges csúcsát eltávolítva már lesz benne Hamilton-kör

A matematika, azon belül a gráfelmélet területén G gráf akkor hipohamiltoni (hypohamiltonian), azaz „majdnem Hamilton-körös”, ha nem rendelkezik Hamilton-körrel, de tetszőleges csúcsát eltávolítva már lesz benne Hamilton-kör. Hasonlóan, egy hypotraceable, azaz „majdnem Hamilton-utas” gráf nem tartalmaz Hamilton-utat, de bármely n − 1 csúcsból álló részhalmazát Hamilton-út köti össze.[1]

Egy (Lindgren 1967) által konstruált hipohamiltoni gráf.

Történet szerkesztés

A hipohamiltoni gráfokat először (Sousselier 1963) vizsgálta. (Lindgren 1967) a korai cikkek közül (Gaudin, Herz & Rossi 1964)-t és (Busacker & Saaty 1965)-t említi, további korai munka a (Herz, Duby & Vigué 1967).

(Grötschel 1980) a kutatási terület nagy részét a következőképp összegzi: „az ilyen gráfokat taglaló cikkek általában hipohamiltoni vagy hipotraceable gráfok egy-egy új osztályát mutatják be, megmutatva hogy léteznek n rendű ilyen gráfok, vagy hogy különös és meglepő tulajdonságokkal rendelkeznek”.

Alkalmazások szerkesztés

A hipohamiltoni gráfok előfordulnak az utazó ügynök problémájának egészértékű programozási megoldásaiban: bizonyos fajta hipohamiltoni gráfok az „utazóügynök-politóp” hiperlapjait határozzák meg; ez az alak az utazó ügynök problémája lehetséges megoldásai halmazának konvex burka, a hiperlapokat pedig a probléma vágási módszerrel való megoldásában használják.[2] (Grötschel 1980) megfigyelése szerint egy gráf hipohamiltonisága meghatározásának számítási bonyolultsága, bár nem ismert a pontos értéke, de valószínűleg magas, ezért a hiperlapok megkeresése is nehéz az egészen kicsi hipohamiltoni gráfokén kívül; szerencsére a legkisebb gráfokból nyerhetők ki a legerősebb egyenlőtlenségek, melyeket ez az alkalmazás igényel.[3]

(Park, Lim & Kim 2007) a hipohamiltonisághoz közel álló fogalmakkal operálva mérik meg a párhuzamos számítástechnika által használt hálózati topológiák hibatűrését.

Tulajdonságok szerkesztés

Minden hipohamiltoni gráf 3-szorosan összefüggő, hiszen két tetszőleges csúcs eltávolítása után egy Hamilton-út marad, ami összefüggő. Léteznek olyan, n-csúcsú hipohamiltoni gráfok, melyek maximális fokszáma n/2, éleik száma pedig kb. n2/4.[4] Nem ismert, hogy létezik-e négyszeresen összefüggő hypohamiltonian gráf, mint ahogy az sem, hogy létezik-e olyan, amelynek nincs 3 fokú csúcsa. Minden síkbarajzolható hipohamiltoni gráfban van viszont legalább egy olyan csúcs, amelyből csak három él indul ki.[5]

 
Thomassen (1974b) 3 girthű hypohamiltonian gráfja.

(Herz, Duby & Vigué 1967) sejtése szerint a hypohamiltonian gráfok girthparamétere 5 vagy több, de ezt cáfolta (Thomassen 1974b), aki talált 3 és 4 bőségű ellenpéldákat is.

Az 1970-es évek elején ismert hypohamiltonian gráfok többnyire a Petersen-gráf általánosításaként, illetve Chvátal flip-flopjainak[6] segítségével álltak elő, és egyikük sem volt síkbarajzolható. Ez motiválta Chvátalt, amikor felvetette, hogy léteznek-e egyáltalán síkbarajzolható hypohamiltonian gráfok ((Chvátal, Klarner & Knuth 1972) 5 dollárt ajánlott fel annak, aki konstruál egyet) és ha igen, vannak-e köztük 3-regulárisak.

Az első síkbarajzolható hypohamiltonian gráfot a Grinberg-tétel felhasználásával 1976-ban találta (Thomassen 1976), ennek 105 csúcsa volt; talált 3, 4 és 5 bőségű ilyen gráfokat és megmutatta, hogy végtelen sok létezik belőlük. 1979-ben (Hatzel 1979) talált egy 57 csúcsú hypohamiltonian síkgráfot. 1993-ban (Holton & Sheehan 1993) tette fel a kérdést, hogy létezik-e ennél kisebb hypohamiltonian síkgráf. (Zamfirescu & Zamfirescu 2007) 48 csúcsú példát, (Wiener & Araya 2009) 42 csúcsút találtak, az eddigi legkisebbet pedig, 40 csúccsal, (Jooyandeh et al. 2013), a Grinberg-tétel alapján végzett számítógépes kereséssel.

2011-ig nem volt ismert, hogy minden elegendően nagy n-re létezik-e n csúcsú hypohamiltonian, illetve hypotraceable síkgráf. (Wiener & Araya 2011) megmutatta, hogy minden n ≥ 76 esetén létezik n csúcsú síkbarajzolható hypohamiltonian gráf, illetve minden n ≥ 180 esetén létezik n csúcsú síkbarajzolható hypotraceable gráf. Ezeket a becsléseket (Jooyandeh et al. 2013) 2014-ben 42-re, illetve 156-ra javította. A legkisebb ismert síkbarajzolható hypotraceable gráf 138 csúcsból áll, (Wiener 2016) almost hypohamiltonian gráfból kiinduló konstrukciója alapján.

A 3-reguláris, síkbarajzolható, hypohamiltonian gráfok közül az elsőt (Thomassen 1981) találta, ennek 94 csúcsa van. 2011-ig nem is sikerült ennél kisebb példát találni és az sem volt ismert, hogy kellően nagy páros n-ekre mindig létezik-e n csúcsú 3-reguláris, hypohamiltonian síkgráf. Mindkét kérdés (Holton & Sheehan 1993) cikkében még a megoldatlan problémák között szerepel. (Aldred et al. 2000) cikkéből azonban következett, hogy nem létezik 42 vagy kevesebb csúcsú ilyen gráf. 2011-ben mindkét kérdést megválaszolta (Wiener & Araya 2011): bemutatott egy 70 csúcsú 3-reguláris hypohamiltonian síkgráfot, ami jelenleg is a legkisebb ismert ilyen tulajdonságú gráf és bizonyította, hogy n ≥ 86 esetén mindig létezik n csúcsú 3-reguláris hypohamiltonian síkgráf; utóbbi korlátot (Zamfirescu 2015) 74-re javította.

Minden páros n ≥ 356 esetre létezik 3-reguláris, síkbarajzolható, hypotraceable gráf (sőt: poliédergráf), ahogy azt (Araya & Wiener 2011) megmutatta.

Ha egy 3-reguláris gráfnak van Hamilton-köre, élei kiszínezhetők három színnel: a Hamilton-kör éleit váltakozó színekkel kiszínezzük (ezt megtehetjük, mert a kézfogás-lemma miatt páros a hosszúsága), a maradék élekre pedig felhasználjuk a harmadik színt. Így aztán egyetlen snarknak (összefüggő, hídmentes, 3-reguláris gráf, 4-es kromatikus számmal) sem lehet Hamilton-köre, és számos ismert snark hipohamiltoni. Minden hipohamiltoni snark ún. bikritikus: bármely két csúcsát eltávolítva a maradék részgráf éleinek színezéséhez három szín elegendő.[7] A részgráf 3-színezése egyszerűen megadható: egy csúcs eltávolításával a maradék csúcsok Hamilton-kört alkotnak. A második csúcs eltávolításával a körből egy út marad, melynek éleit két színnel váltakozva kiszínezhetjük. A maradék élek párosítást alkotnak, ezért a harmadik szín elegendő hozzájuk.

Egy 3-reguláris gráf 3-színezésének a színosztályai olyan három párosítást alkotnak, melyben minden él pontosan egy párosításhoz tartozik.. A hipohamiltoni snarkoknak nincs ilyen párosításuk, de (Häggkvist 2007) sejtése szerint éleik hat párosításba oszthatók oly módon, hogy minden él pontosan két párosításba tartozzon. Ez a Berge–Fulkerson-sejtés speciális esete, mely kimondja, hogy bármely snarknak hat ilyen tulajdonságú párosítása van.

A hipohamiltoni gráfok nem lehetnek párosak: egy páros gráfban egy csúcs törlésével csak akkor jön létre Hamilton-körű részgráf, ha a gráf két színosztálya közül a nagyobbikba tartozik. Minden páros gráf előáll azonban valamely hipohamiltoni gráf feszített részgráfjaként.[8]

Példák szerkesztés

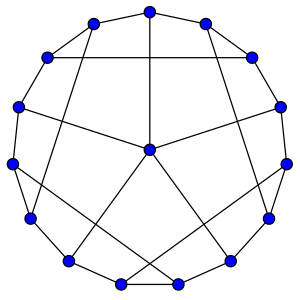
A legkisebb hypohamiltonian gráf a Petersen-gráf (Herz, Duby & Vigué 1967). Általánosabban, a GP(n,2) általánosított Petersen-gráf akkor hypohamiltonian, amikor n kongruens 5 (mod 6);[9] maga a Petersen-gráf az n = 5 esetben áll elő.

(Lindgren 1967) talált egy másik végtelen hipohamiltoni gráfosztályt, melyben a csúcsok száma kongruens 4 (mod 6). Lindgren konstrukciója egy 3 (mod 6) hosszúságú körből és egyetlen központi csúcsból áll; a központi csúcsot összeköti a kör minden harmadik csúcsával (ezeket nevezi küllőknek) és a küllő-végpontoktól kettő-kettő távolságra lévő csúcsokat pedig egymással. Lindgren konstrukciója esetében is a legkisebb előállítható gráf a Petersen-gráf.

További végtelen családokat ír le (Bondy 1972), (Doyen & van Diest 1975) és (Gutt 1977).

Leszámlálás szerkesztés

Václav Chvátal 1973-as bizonyítása szerint elegendően nagy n-re létezik n csúcsú hipohamiltoni gráf. A későbbi felfedezéseket is figyelembe véve,[10] jelenlegi tudásunk szerint az „elegendően nagy” azt jelenti, hogy minden n ≥ 18 értékre léteznek ilyen gráfok. A legfeljebb 17 csúcsú hipohamiltoni gráfok teljes listája ismert:[11] ezek a 10 csúcsú Petersen-gráf, a (Herz 1968) számítógépes keresése által fellelt 13, illetve 15 csúcsú gráf és négy 16 csúcsú gráf. Legalább tizenhárom 18 csúcsú hipohamiltoni gráf létezik. (Chvátal 1973) flip-flop módszerét a Petersen-gráfra és a virág-snarkra alkalmazva megmutatható, hogy a hypohamiltonian gráfok, azon belül is a hypohamiltonian snarkok száma a csúcsok számának exponenciális függvényében növekszik.[12]

Hypotraceable gráfok szerkesztés

Az első, 40 csúcsú hypotraceable gráfot Horton találta 1976-ban (Thomassen 1976), az eddigi legkisebb, 34 csúcsú hypotraceable gráf felfedezése (Thomassen 1976) érdeme. A legkisebb hypotraceble gráf méretére nincs jó alsó becslés, részben azért, mert ezeket a gráfokat eddig Thomassen két módszerét felhasználva hypohamiltonian gráfokból állították elő. Az ugyanakkor (Jooyandeh et al. 2013) alapján ismert, hogy az n ≥ 42 esetekre létezik n csúcsú hypotraceable gráf.

Általánosítások szerkesztés

A hipohamiltoni és hypotraceable gráfok irányított gráf-analógiáival több szerző is foglalkozott már.[13]

A hipohamiltoni gráfok egy ekvivalens definíciója szerint ezek a gráfok, melyek leghosszabb köre n − 1 hosszúságú és az összes leghosszabb kör metszete üres. (Menke, Zamfirescu & Zamfirescu 1998) azokat a gráfokat vizsgálta, melyekben a leghosszabb körök metszete szintén üres, de leghosszabb kör rövidebb n − 1-nél. (Herz 1968) úgy definiálja egy gráf cyclability paraméterét, mint az a legnagyobb k szám, melyre bármely k csúcs ugyanabba a körbe tartozik; a hypohamiltonian gráfok pontosan azok a gráfok, melyek cyclability paramétere n − 1. Hasonlóan (Park, Lim & Kim 2007) definíciója szerint egy gráf ƒ-fault hamiltonian (ƒ hibával hamiltoni), ha a legfeljebb ƒ csúcs eltávolításával kapott részgráfnak van Hamilton-köre. (Schauerte & Zamfirescu 2006) azokat a gráfokat vizsgálja, melyekben a cyclability értéke n − 2.

Foglalkoznak továbbá almost hypohamiltonian és almost hypotraceable gráfokkal is.

Fordítás szerkesztés

  • Ez a szócikk részben vagy egészben a Hypohamiltonian graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek szerkesztés

  1. ↑ (Kapoor, Kronk & Lick 1968); (Kronk 1969); (Grünbaum 1974); (Thomassen 1974a).
  2. ↑ (Grötschel 1977); (Grötschel 1980); (Grötschel & Wakabayashi 1981).
  3. ↑ (Goemans 1995).
  4. ↑ (Thomassen 1981).
  5. ↑ (Thomassen 1978).
  6. ↑ (Chvátal 1973)
  7. ↑ (Steffen 1998); (Steffen 2001).
  8. ↑ (Collier & Schmeichel 1977).
  9. ↑ (Robertson 1969) igazolta, hogy ezeknek a gráfoknak nincs Hamilton-körük, pedig egyszerűen ellenőrizhető, hogy az egy csúcs kitörlésével kapott gráfoknak viszont van. Lásd (Alspach 1983) munkáját a Hamilton-kör nélküli általánosított Petersen-gráfok osztályozásáról.
  10. ↑ (Thomassen 1974a); (Doyen & van Diest 1975).
  11. ↑ (Aldred, McKay & Wormald 1997). Lásd még (A141150 sorozat az OEIS-ben).
  12. ↑ (Skupień 1989); (Skupień 2007).
  13. ↑ (Fouquet & Jolivet 1978); (Grötschel & Wakabayashi 1980); (Grötschel & Wakabayashi 1984); (Thomassen 1978).

További információk szerkesztés

A lap eredeti címe: „https://hu.wikipedia.org/w/index.php?title=Hipohamiltoni_gráf&oldid=26217711”