Periferikus kör
A matematika, azon belül a gráfelmélet területén egy irányítatlan gráf periferikus köre vagy periferiális köre (peripheral circuit) olyan kör, ami nem választja el egymástól a gráf különböző részeit. A periferikus köröket (vagy Tutte sajátos nevezéktana szerint, periferikus sokszögeket) elsőként (Tutte 1963) vizsgálta. Fontos szerepet játszanak a síkbarajzolható gráfok jellemzésében és a nem-síkgráfok körtereinek előállításában.[1]
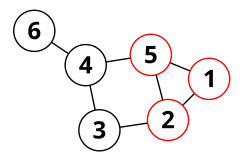
Definíciók
szerkesztésEgy gráf periferikus köre több, egymással ekvivalens módon definiálható:
- periferikus, ha összefüggő gráf egyszerű köre, mely azzal a tulajdonsággal rendelkezik, hogy bármely két és éléhez tartozik olyan -beli út, ami -gyel kezdődik, -ben végződik és egyetlen belső csúcsa sem tartozik -hez.[2]
- periferikus, ha olyan feszített kör, melyre igaz, hogy a csúcsainak és éleinek törlésével kapott részgráf összefüggő.[3]
- Ha a -nek tetszőleges részgráfja, egy hídja (bridge)[4] alatt azon minimális részgráfját értjük, ami -vel éldiszjunkt és minden csatolódási pontja (A és élein is rajta lévő csúcsa) -hez tartozik.[5] Egy egyszerű kör akkor periferikus, ha pontosan egy hídja van.[6]
A fenti definíciók egyenértékűségét nem nehéz belátni: akár a egy összefüggő részgráfjának (az őt -vel összekötő élekkel együtt), akár egy kör annak feszített körségét megakadályozó húrjának hídnak kell lenniük, továbbá az éleken értelmezett bináris reláció ekvivalenciaosztályának, melyben két él akkor van egymással relációban, ha egy olyan út két végén találhatók, melynek nincsenek belső csúcsai -ben.[7]
Tulajdonságok
szerkesztésA periferikus körök megjelennek a poliédergráfok, azaz a 3-szorosan csúcsösszefüggő síkbarajzolható gráfok elméletében. Minden síkbarajzolható gráf, minden síkba rajzolásának azon tartományainak, melyek feszített körök, periferikus köröknek kell lenniük. Egy poliédergráfban minden tartomány periferikus kör, és minden periferikus kör tartomány.[8] Ebből a tényből következik, hogy (a kombinatorikus ekvivalencia, a külső tartomány választása és a sík orientációja erejéig) minden poliédergráf egyedi síkba ágyazással rendelkezik.[9] A síkbarajzolható gráfok körterét a síkba rajzolás tartományai generálják, míg síkba nem rajzolható gráfok esetében a periferikus körök játszanak hasonló szerepet: bármely 3-szorosan csúcsösszefüggő véges gráf körterét a periferikus körök generálják.[10] Az eredmény kiterjeszthető olyan végtelen gráfokra is, melyek lokálisan végesek.[11] Az előzőekből az is következik, hogy minden 3-szorosan csúcsösszefüggő gráf garantáltan tartalmaz periferikus köröket. Léteznek olyan 2-összefüggő gráfok, amik nem tartalmaznak periferikus köröket (ilyen például a teljes páros gráf, melynek minden köréhez két híd tartozik), de ha egy 2-összefüggő gráf minimális fokszáma 3, akkor legalább egy periferikus kört tartalmaznia kell.[12] A 3-összefüggő gráfok periferikus körei lineáris időben megkereshetők, ezért síkbarajzolhatósági tesztekben is felhasználják őket.[13] Kiterjesztették őket a nem szeparáló fülfelbontások általánosabb fogalmára is. Egyes síkbarajzolhatóságot tesztelő algoritmusokban hasznos lehet nem periferikus kört keresni a probléma kisebb alproblémákra osztásához. Egy háromnál kisebb ciklikus rangú 2-összefüggő gráf (amilyen egy körgráf vagy egy thétagráf) minden kör periferikus, de a legalább három ciklikus rangú 2-összefüggő gráfokban már lennie kell nem periferikus körnek is, ami lineáris időben megkereshető.[14] (Seymour & Weaver 1984) a merev körű gráfok általánosításaiként úgy definiálja a lekötött gráfokat, hogy a gráfok, melyek minden periferikus köre háromszög. Karakterizációjuk alapján ezek a gráfok, melyek előállnak merev körű gráfok és maximális síkgráfok klikkösszegeiként.[15]
Kapcsolódó fogalmak
szerkesztésA periferikus köröket nevezik nem elválasztó köröknek vagy nem szeparáló köröknek is,[2] de ez a kifejezés kétértelmű, mivel két hasonló, de eltérő fogalomra is használják: egyszerű körök, melyek eltávolítása után nem esik szét a megmaradó gráf,[16] avagy topologikusan beágyazott gráfnál olyan kör, mely mentén végigvágva az adott felületet, melybe a gráf be van ágyazva, a felület nem esik szét.[17] Matroidok esetében egy nem szeparáló kör a matroid olyan köre (tehát egy minimális függő halmaza), melyet kitörölve egy kisebb, összefüggő (kisebb matroidok direkt összegeként fel nem írható) matroid marad.[18] Ezek a periferikus körökkel analóg, de nem teljesen megegyező fogalmak, még a grafikus matroidok (matroidok, melyek körei a gráf egyszerű köreinek felelnek meg) esetében sem. Például a teljes páros gráf minden köre periferikus (egyetlen hídja van, egy két élből álló út), de a híd által alkotott grafikus matroid nem összefüggő, így a grafikus matroid egyetlen körére sem igaz, hogy nem szeparáló.
Fordítás
szerkesztés- Ez a szócikk részben vagy egészben a Peripheral cycle című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
szerkesztés- ↑ Tutte, W. T. (1963), "How to draw a graph", Proceedings of the London Mathematical Society, Third Series 13: 743–767, DOI 10.1112/plms/s3-13.1.743.
- ↑ a b Di Battista, Giuseppe; Eades, Peter & Tamassia, Roberto et al. (1998), Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, pp. 74–75, ISBN 978-0-13-301615-4.
- ↑ Ez lényegében a (Bruhn 2004) által is használt definíció. A különbség annyi, hogy Bruhn megkülönbözteti az esetet, amikor -nek eleve vannak izolált csúcsai attól, amikor a eltávolításától esik szét a gráf.
- ↑ Nem összetévesztendő az elválasztó éllel, ami egy másik fogalom.
- ↑ Tutte, W. T. (1960), "Convex representations of graphs", Proceedings of the London Mathematical Society, Third Series 10: 304–320, DOI 10.1112/plms/s3-10.1.304.
- ↑ Ez a periferikus körök (Tutte 1963) által leírt eredeti definíciója. (Seymour & Weaver 1984) a periferikus köröket ugyanúgy definiálják, de a híd más definíciójával, ami inkább emlékeztet a periferikus körök feszített körös definíciójára.
- ↑ Lásd pl. a Theorem 2.4-et itt: (Tutte 1960), ami megmutatja, hogy a hidak csúcshalmazai úttal összekötöttek, továbbá (Seymour & Weaver 1984)-et a hidak húrokkal és összefüggő komponensekkel való definiáláshoz, valamint (Di Battista et al. 1998)-t a hidak éleken értelmezett bináris reláció ekvivalenciaosztályaként történő definíciójához.
- ↑ Lásd (Tutte 1963), Theorems 2.7 és 2.8.
- ↑ Lásd a Theorem 2.8-at követő megjegyzéseket itt: (Tutte 1963). Tutte megfigyelése szerint ez a tény már számukra is ismert volt: Whitney, Hassler (1932), "Non-separable and planar graphs", Transactions of the American Mathematical Society 34 (2): 339–362, DOI 10.2307/1989545.
- ↑ (Tutte 1963), Theorem 2.5.
- ↑ Bruhn, Henning (2004), "The cycle space of a 3-connected locally finite graph is generated by its finite and infinite peripheral circuits", Journal of Combinatorial Theory, Series B 92 (2): 235–256, DOI 10.1016/j.jctb.2004.03.005.
- ↑ Thomassen, Carsten & Toft, Bjarne (1981), "Non-separating induced cycles in graphs", Journal of Combinatorial Theory, Series B 31 (2): 199–224, DOI 10.1016/S0095-8956(81)80025-1.
- ↑ Schmidt, Jens M. (2014), The Mondshein Sequence, pp. 967-978, DOI 10.1007/978-3-662-43948-7_80.
- ↑ (Di Battista et al. 1998), Lemma 3.4, pp. 75–76.
- ↑ Seymour, P. D. & Weaver, R. W. (1984), "A generalization of chordal graphs", Journal of Graph Theory 8 (2): 241–251, DOI 10.1002/jgt.3190080206.
- ↑ Pl. lásd Borse, Y. M. & Waphare, B. N. (2008), "Vertex disjoint non-separating cycles in graphs", The Journal of the Indian Mathematical Society, New Series 75 (1-4): 75–92 (2009).
- ↑ Lásd pl. Cabello, Sergio & Mohar, Bojan (2007), "Finding shortest non-separating and non-contractible cycles for topologically embedded graphs", Discrete and Computational Geometry 37 (2): 213–235, DOI 10.1007/s00454-006-1292-5.
- ↑ Maia, Bráulio, Junior; Lemos, Manoel & Melo, Tereza R. B. (2007), "Non-separating circuits and cocircuits in matroids", Combinatorics, complexity, and chance, vol. 34, Oxford Lecture Ser. Math. Appl., Oxford: Oxford Univ. Press, pp. 162–171, DOI 10.1093/acprof:oso/9780198571278.003.0010.