Lorentz-erő

A Lorentz-erő az elektromágneses térben egy elektromos töltésre ható erő. Ennek két komponense közül az elektromos arányos és egyirányú az elektromos térerősséggel, a mágneses arányos és merőleges a mágneses indukcióra és a töltés sebességére. A Lorentz-erő Hendrik Lorentz (1853 – 1928) holland fizikus nevét viseli.

A Lorentz-erő

A mágneses erő az az erő, amely a mágnesesség miatt gyorsulásra késztethet a hatása alatt lévő tömeget.

Egy erőt konzervatív erőnek nevezünk, ha kifejezhető egy potenciál gradienseként (egy konzervatív erő állandó irányú, és nagyságú erőt jelent). Ilyenek például a gravitációs erő, az elektrosztatikus erő, stb. A nemkonzervatív erők például a súrlódási erők, stb. A mágneses erő nem konzervatív. A nemkonzervatív erőket disszipatív erőknek is nevezik. A disszipatív erő energiaveszteséget okoz.

Mozgó elektromos töltés (elektromos áram) vagy az elektromos mező változása létrehozhat mágneses mezőt (mágneses tér, mágneses erőtér). A mágneses mezőt jellemző fizikai mennyiség a mágneses fluxussűrűség, mértékegysége a tesla (Vs / m2).

A mágneses erőtér által kifejtett munkát általában nem a megszokott SI-beli erő mértékegységgel (newton) jellemzik, hanem közvetett módon a mágneses térerősséggel, mert azt sokkal könnyebb mérni.

A mágneses erőtér mértékének kifejezésére az SI-mértékegységrendszerben a tesla, a CGS rendszerben a gauss mértékegységeket használják [1 Tesla = 10 000 Gauss, másképpen 10 G = 1 mT (1 millitesla) ]. A gaussban (rövidítve: G) megadott mágneses térerősség egységét az 1 cm² területen áthaladó mágneses erővonalak száma jelenti. Viszonyításképpen néhány adat a mágneses erő mértékére: a Föld mágneses mezője kb. 0,5 G erősségű, az átlagos hűtőmágnesek 35-200 G, az iparban használatos eszközök 300-5000 G erősségűek. Az MRI vizsgálat során 200 000 G erősségű mágneses teret alkalmaznak.

A lokális mágneses erőt többnyire magnetométerrel mérik, amely valójában a mágneses térerősséget méri. Távolabbi mágneses hatásokat rádióteleszkópokkal lehet kimutatni.

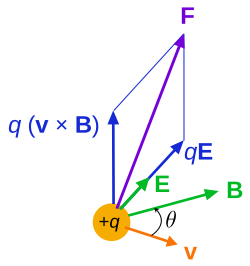
A Lorentz-erő:

$F=q(E+v\times B)$

Ha E=0, azaz ha az elektromos mező azonosan zérus, akkor a Lorentz-erő a mágneses erő:

$F=q(v\times B)$

ahol

F az erő (N)

E az elektromos térerősség (V/m)

B a mágneses indukció (T)

q a részecske elektromos töltése (C)

v a részecske pillanatnyi sebessége (m/s)

és az × a vektoriális szorzás jele.

Az erő nagysága

A Lorentz-erő nagysága

${\vec {\mathbf {F} }}=q\left({\vec {\mathbf {E} }}+{\vec {\mathbf {v} }}\times {\vec {\mathbf {B} }}\right)$

ahol q az elektromos töltés, E az elektromos térerősség, B a mágneses indukció és v az elektromos töltés sebessége. A Lorentz-erő mágneses komponense nem végez munkát, a mágneses tér egy mozgó töltött részecske kinetikus energiáját nem változtatja meg.

Áramjárta vezetőre ható erő

A Lorentz-erő a mágneses tér által kifejtett erő egy áramjárta vezetőre. Ha egy elektromos vezetékbe áramot vezetünk, magában a vezetékben elektromos töltés halad végig. Emellett azonban jelen vannak szabadon mozgó (nem a vezetékben lévő) töltött részecskék, amikre szintén erő hat, ha azok mágneses térbe kerülnek.

A Lorentz-erő függ:

• Mágneses indukcióvektor nagyságától (B)
• Áramerősségtől (I)
• Vezető hosszától (L)

$F=B\cdot I\cdot l$

• Értéke maximális, ha a mágneses indukcióvonalak merőlegesek a vezetőre.
• Értéke zérus, ha a mágneses indukcióvonalak párhuzamosak a vezetővel.

Mágneses Lorentz-erő

Ha a mágneses térben egy adott P ponton t idő alatt N számú, egyenként Q töltésű részecske halad keresztül azonos irányban és azonos sebességgel, akkor az általuk képviselt áramerősség: I=NQ/t. A v sebességű Q töltés tegyen meg l=vt utat a B indukciójú térben. Ekkor az N számú részecskére ható erő:

$F=I(l\times B)=(NQ/t)(vt)\times B=NQ(v\times B)$

Ily módon az egyetlen részecskére ható erő:

$F=Q(v\times B)$

Ezt az erőt mágneses Lorentz-erőnek nevezzük. A fenti összefüggés a megfigyelt kísérleti eredményekkel teljes megegyezésben van.

Az F erő nagysága:

$F=QvB\sin \theta$

ahol θ a v és B közötti szöget jelenti.

A mágneses erő eltűnik (zérus), ha v=0, valamint, ha v egybe esik (párhuzamos vagy ellentétes) a B vektor irányával. A sebességre és a mágneses indukcióra merőleges eltérítő erő maximális, ha v merőleges B-re: $F_{max}=QvB$.

Források

• ↑ Fizikai kislexikon: szerk.: Dr. Szilágyi Miklós: Fizikai Kislexikon. Műszaki Könyvkiadó. 963 10 1695 1 (1977) 
• Hevesi Imre: Elektromosságtan
• Dr.Fodor György-Dr. Vágó István: Villamoságtan, 12.füzet: Statikus és stacionárius tér, Tankönyv Kiadó, Budapest, 1975
• Simonyi Károly: Villamosságtan. Akadémiai Kiadó, Budapest, 1962

További információk

• Magyarított interaktív Java szimuláció a Lorentz-erőről Szerző: Wolfgang Bauer