Standard modell

A részecskefizika standard modellje (gyakran magyarban is nagy kezdőbetűkkel írják: Standard Modell (SM), ejtsd sztenderd modell) az elektromágneses, a gyenge és erős kölcsönhatást, valamint az alapvető elemi részecskéket leíró kvantumtérelmélet. Összhangban van a kvantummechanikával és a speciális relativitáselmélettel. Majdnem minden kísérleti teszt igazolja jóslatait, a korábbi kivételek legjelentősebbikét, a Higgs-bozon létezését már igazolták. A modell közvetlen előzményei és részei az elektrogyenge kölcsönhatások modellje (Glashow–Weinberg–Salam-modell) és az erős kölcsönhatások elmélete, a kvantum-színdinamika (QCD).

Az elemi részecskék standard modellje

A standard modell

Részecsketípusai

Az elemi részecskék kölcsönhatásainak egyszerűsített ábrázolása a standard modell szerint

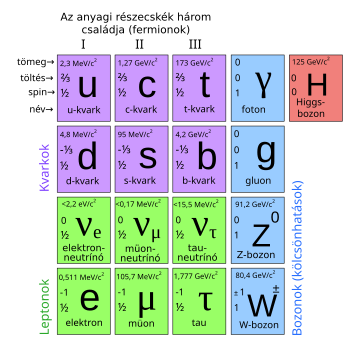
A modell alapvető részecskéi között vannak egyrészt az anyagot felépítő ún. anyagi részecskék. Ezek mind feles spinűek, azaz fermionok. A kvarkok és leptonok tartoznak ide. A fermionokra érvényes Pauli-elv miatt nem omlik össze egy anyaghalmaz, hanem kénytelen egy bizonyos térfogatot kitölteni. A kvarkok az erős és elektrogyenge kölcsönhatásban is részt vesznek, míg a leptonok csak az elektrogyengében.

A másik típusú részecskék a – kölcsönhatásokat – közvetítő részecskék. Az elektrogyenge kölcsönhatást közvetítő foton, két W-bozon, és a Z-bozon valamint az erős kölcsönhatást közvetítő gluonok tartoznak ide. Ezek mind egyes spinűek, azaz bozonok, spinjük miatt vektorbozonoknak is mondjuk őket. Bozonokra nincs Pauli-kizárás, ezek közül akárhány lehet azonos kvantumállapotban, ami nagyon sok bozonnal nagyon kifinomult kölcsönhatást tesz lehetővé.

A harmadik típusú részecske a már kísérletileg is igazolt nulla spinű Higgs-bozon, amiből a standard modellben egy van, de a kiterjesztett elméletekben több. A Higgs-bozon az önmagával és a többi részecskével való kölcsönhatásaival tömeget „kölcsönöz” az anyagi részecskéknek és a közvetítő részecskék egy részének.

Szimmetriája és sérülése

A modell egy mértékelmélet, amelynek a Lagrange-függvénye tehát lokálisan invariáns egy mértékcsoport transzformációival szemben. A mértékcsoport esetünkben az SU(3)×SU(2)×U(1). A közvetítő bozonokat a modell mértékterei írják le, ezért őket mértékbozonoknak is hívjuk. A mértékterek a klasszikus elektrodinamika (skalár- és vektor)potenciáltereinek kvantumtérelméleti megfelelői.

A Higgs-bozon nélkül azonban a standard modell, ami az említett mértékcsoporttal szemben mértékinvariáns, nem nyújtaná reális leírását a világnak. A mértékinvariancia fenntartása esetén ugyanis a modell részecskéinek nem lehetne tömegük, márpedig az elemi részecskék többségének van tömege. Ha ezeket a tömegeket kézzel beletennénk a Lagrange-függvénybe – amiből a hatáselv segítségével a mozgásegyenletek származtathatók – akkor ezzel nemcsak a mértékinvarianciát rontanánk el – amit el is kell rontanunk, hiszen az SU(2)-szimmetria a világnak szemmel láthatóan nem egzakt szimmetriája, hanem egy fontos elvi problémába is ütköznénk. Az elmélet nem lenne renormálható, azaz a számítások közben fellépő végtelen mennyiségeket nem lehetne konzisztens módon eltávolítani hozzárendelve őket véges számú fizikai mennyiséghez – például töltés –, mintegy „lenyeletve” őket velük.

Ennek orvoslására találta ki Peter Higgs még a standard modell felépítése előtt a Higgs-mechanizmust, ami egy mértékinvariáns skalártér nem mértékinvariáns alapállapotán keresztül spontán sérti a mértékinvarianciát. Esetünkben csak egy részét, az alapállapot ugyanis mértékinvariáns marad egy SU(3)×U(1) mértékcsoporttal szemben, azaz csak a gyenge kölcsönhatás mértékinvarianciája sérül, alacsony energián, azon, amelyen mi is látjuk a világot. Nagy energiájú folyamatoknál a szimmetria kezd helyreállni. A sértés előtti és utáni U(1) szimmetria egyébként nem ugyanaz az U(1), előtte a hipertöltéshez, utána az elektromos töltéshez kapcsolódó szimmetriáról van szó. Valójában tehát nem az SU(2) sérül a semmire, hanem az SU(2)×U(1) szimmetria egy másik U(1)-re.

A Higgs-mechanizmuson keresztül a sértett szimmetriához tartozó mértékbozonok és a hozzá tartozó kölcsönhatásban részt vevő anyagi részecskék tömeget nyernek a Higgs-bozon belső átrendeződése folytán. Elveszíti ugyanis három szabadsági fokát az eredeti négy közül, s ez a három csatlakozik a sértett gyenge kölcsönhatás így tömeget nyerő három mértékbozonjához.

Részecskecsaládok

Az anyagi részecskéket három családba rendezhetjük, mindegyikbe a hat-hatféle kvarkból (kvarkízből) ill. leptonból (leptonízből) kettő-kettőt téve (ld. a táblázatot). A LEP kísérleteinek sikerült 1989-ben bebizonyítaniuk, hogy csak három család létezik. Ezt a Z-bozon szélességének mérésével érték el. A standard modell nem nyújt azonban elméleti magyarázatot arra, miért van ez így. Erre a nagy egyesített elmélettől várunk magyarázatot. Anyagi világunk túlnyomó többségét az első család fermionjai építik fel.

Táblázat

Balkezes Standard modellben

1. család
Fermion (Balkezes)	Jelölés	Elektromos töltés	Gyenge töltés*	Gyenge izospin	Hipertöltés	Színtöltés*	Tömeg**
Elektron	$e$	−1	$\mathbf {2}$	−1/2	−1/2	$\mathbf {1}$	0.511 MeV
Elektron-neutrínó	$\nu _{e}$	0	$\mathbf {2}$	+1/2	−1/2	$\mathbf {1}$	< 50 eV
Pozitron	$e^{c}$	+1	$\mathbf {1}$	0	+1	$\mathbf {1}$	0.511 MeV
Elektron-antineutrínó	$\nu _{e}^{c}$	0	$\mathbf {1}$	0	0	$\mathbf {1}$	< 50 eV
Up kvark	$u$	+2/3	$\mathbf {2}$	+1/2	+1/6	$\mathbf {3}$	~5 MeV ***
Down kvark	$d$	−1/3	$\mathbf {2}$	−1/2	+1/6	$\mathbf {3}$	~10 MeV ***
Anti-up antikvark	$u^{c}$	−2/3	$\mathbf {1}$	0	−2/3	$\mathbf {\bar {3}}$	~5 MeV ***
Anti-down antikvark	$d^{c}$	+1/3	$\mathbf {1}$	0	+1/3	$\mathbf {\bar {3}}$	~10 MeV ***
2. család
Fermion (balkezes)	jelölés	Elektromos töltés	Gyenge töltés*	Gyenge izospin	Hipertöltés	Színtöltés*	Tömeg**
Müon	$\mu$	−1	$\mathbf {2}$	−1/2	−1/2	$\mathbf {1}$	105.6 MeV
Müon-neutrínó	$\nu _{\mu }$	0	$\mathbf {2}$	+1/2	−1/2	$\mathbf {1}$	< 0.5 MeV
Antimüon	$\mu ^{c}$	+1	$\mathbf {1}$	0	+1	$\mathbf {1}$	105.6 MeV
Müon-antineutrínó	$\nu _{\mu }^{c}$	0	$\mathbf {1}$	0	0	$\mathbf {1}$	< 0.5 MeV
Bájos kvark	$c$	+2/3	$\mathbf {2}$	+1/2	+1/6	$\mathbf {3}$	~1.5 GeV
Ritka kvark	$s$	−1/3	$\mathbf {2}$	−1/2	+1/6	$\mathbf {3}$	~100 MeV
Anti-bájos antikvark	$c^{c}$	−2/3	$\mathbf {1}$	0	−2/3	$\mathbf {\bar {3}}$	~1.5 GeV
Anti-ritka antikvark	$s^{c}$	+1/3	$\mathbf {1}$	0	+1/3	$\mathbf {\bar {3}}$	~100 MeV
3. család
Fermion (balkezes)	Jelölés	Elektromos töltés	Gyenge töltés*	Gyenge izospin	Hipertöltés	Színtöltés*	Tömeg**
Tau lepton	$\tau$	−1	$\mathbf {2}$	−1/2	−1/2	$\mathbf {1}$	1.784 GeV
Tau-neutrínó	$\nu _{\tau }$	0	$\mathbf {2}$	+1/2	−1/2	$\mathbf {1}$	< 70 MeV
Anti-Tau	$\tau ^{c}$	+1	$\mathbf {1}$	0	+1	$\mathbf {1}$	1.784 GeV
Tau-antineutrínó	$\nu _{\tau }^{c}$	0	$\mathbf {1}$	0	0	$\mathbf {1}$	< 70 MeV
Top kvark	$t$	+2/3	$\mathbf {2}$	+1/2	+1/6	$\mathbf {3}$	173 GeV
Bottom kvark	$b$	−1/3	$\mathbf {2}$	−1/2	+1/6	$\mathbf {3}$	~4.7 GeV
Anti-top antikvark	$t^{c}$	−2/3	$\mathbf {1}$	0	−2/3	$\mathbf {\bar {3}}$	173 GeV
Anti-bottom antikvark	$b^{c}$	+1/3	$\mathbf {1}$	0	+1/3	$\mathbf {\bar {3}}$	~4.7 GeV
* – Ezek nem közönséges abeli töltések, amelyek összeadhatók egymással, hanem Lie-csoportok csoportreprezentációinak címkéi. ** – A tömeg valójában a balkezes és jobbkezes fermionok közötti csatolás. Például az elektron tömege valójában a balkezes elektron és a jobbkezes elektron – ami a balkezes pozitron antirészecskéje – közötti csatolás. A neutrinók viszont nagy keveredést tanúsítanak a tömegcsatolásuk során az egyes ízek között, úgyhogy nem pontos dolog ízbázison neutrínó tömegről beszélni, vagy azt sugallni, hogy a balkezes és jobbekezes neutrínónak ugyanaz a tömege, mint ez a táblázat is teszi. *** – Amit valójában mérünk, az a hadronok tömege, valamint számos hatáskeresztmetszet. Mivel a kvarkok nem elkülöníthetők a kvarkbezárás miatt, az itt levő értékről feltesszük, hogy az a kvark tömege a QCD renormálási skálájánál (fázisátmenet). Ezen érték kiszámításához rács mértékelméleti számításokat kell végezni a hadronspektrum meghatározásához, kipróbálva számos tömegértéket, amíg a modell nem ad a kísérleti adatokhoz közeli értékeket. Mivel az első család kvarkjai jelentősen a QCD-skála alatt vannak, a bizonytalanságok meglehetősen nagyok. Történetesen a legutóbbi rács-QCD számítások a táblázatban foglaltaknál jelentősen kisebb értékeket adnak.

Előrejelzések és tesztjeik

A standard modell megjósolta a W- és Z-bozonok, a gluonok, a top kvark és a charm kvark létezését mielőtt felfedezték volna azokat. Azok a paramétereik, melyeket előre tudtak jelezni nagyon jól egyeztek a kísérletileg mért értékekkel.

A CERN nagy elektron-pozitron ütköztetőgyűrűje több előrejelzést vizsgált a Z-bozon bomlásával kapcsolatban, és egyezőnek találta azokat.

Pár adatot olvashatunk alább arról, hogy milyen számszerű értékeket jelzett előre a modell, és milyen értékeket mértek később:

Mennyiség	Mért érték (GeV)	SM jóslat (GeV)
W-bozon tömeg	80,4120±0,0420	80,3900±0,0180
Z-bozon tömeg	91,1874±0,0021	91,1874±0,0021

Feynman-diagramok

A kölcsönhatásokat Feynman-diagramon, vagy ennek matematikai modelljén, Feynman-gráfon szokták ábrázolni. A részecskéket különböző vonalak jelképezik, és a vonalak találkozása egy kölcsönhatást jelöl. A fermionokat egyenesek, a gluonokat rugósszerű vonalak, bozonokat hullámvonalak jelölik.

A standard modell hiányosságai

A standard modell nem tartalmazza a részecskék világában kis jelentőségű gravitációt és nem egyesíti az erős kölcsönhatást sem az elektrogyenge kölcsönhatással, amilyen módon az elektrogyenge elmélet egyesíti az elektromágneses kölcsönhatást és a gyenge kölcsönhatást. A standard modell nem képes számot adni az elméletben szereplő 19 (!) szabad paraméter értékéről (részecsketömegek, keverési szögek, csatolási erősségek). A standard modell komplikációi számos problémába csoportosíthatók:

• 1. mértékprobléma: A standard modell három mértékcsoport direkt szorzata, amelyek közül csak az elektrogyenge rész paritássértő. A modell tartalmazza, de nem magyarázza az elektromos töltés kvantáltságát (ez nagyon fontos az atomok semlegessége szempontjából). Megoldást jelenthet többek között a nagy egyesített elmélet (GUT) vagy a mágneses monopólusok létezése.

• 2. fermionprobléma: A közönséges földi anyagok az első családból megkonstruálhatók. Nem tudjuk, miért van három család, amelyek közül a másik kettő az elsőnek nehéz másolata. Nem ad magyarázatot a fermionok tömegére, amelyek ráadásul öt nagyságrendi különbségen belül szórnak. Megoldást jelenthetnek összetett fermionok, családszimmetriák, extra téridő dimenziók, például szuperhúrok.

• 3. Higgs/hierarchia-probléma: A standard modell egy Higgs-bozont tartalmaz – amit 2012, július 4-én jelentettek be, hogy sikerült ki is mutatni – a W-,Z- és fermiontömegek generálása céljából. A Higgs-bozon tömege nem lehet túl nagy (elméleti megfontolások és a kísérleti eredmények alapján <1 TeV), mert különben túl erős lenne az önkölcsönhatása (A 2012, júl. 4-én bejelentett érték 125-126 GeV). A magasabb rendbeli számolások viszont divergens járulékot adnak a tömegéhez, és a végtelen értéket csak úgy lehet elkerülni, ha történik valami magasabb energiákon, azaz valami új elmélet kezd érvényessé válni. Ilyenek lehetnek a nagy egyesített elméletek, de ez 10¹⁴ GeV nagyságú Higgs-tömeghez vezetne, vagy a gravitáció belépése, ami viszont a Planck-tömeg (10¹⁹ GeV) nagyságúhoz, azaz 1 TeV-nél jóval nagyobbakhoz. Megoldást összetett W- és Z-bozonok (de ezzel eldobnánk a rendkívül sikeres SU(2)×U(1) elektrogyenge elméletet), Higgs-bozon helyett fermion kötött állapotok, a technicolor vagy összetett Higgs-részecskék jelenthetnének. A talán legnépszerűbb megoldást a szuperszimmetria létezése jelentené.

• 4. erős CP-probléma: A standard modellbe bevezethető egy P-, T- és CP-sértő tag, ami a neutronnak elektromos dipólmomentumot adna. Ennek létező kísérleti limitjei viszont a bevezetendő tag együtthatója 10⁻¹⁰ nagyságrendű lenne. Ez a kis szám nem érthető, ahogy általában a sok nagyságrenddel eltérő paraméterek nem elfogadhatóak. A megoldást a CP-sértés jelenlegi explicit mechanizmusa helyett például egy spontán sértett extra U(1) szimmetria bevezetése jelenthetné, ami viszont egy új részecske, az axion megjelenésével járna.

• 5. gravitonprobléma: a gravitáció kívül esik a standard modellen és az általános relativitáselméletet – ami nem kvantumelmélet – nem is lehet a többi kölcsönhatás elmélete módjára kvantumtérelméletté tenni. Egy másik probléma a kozmológiai állandóé. Ez a vákuum energiájának tekinthető, aminek értéke a spontán szimmetriasértés során a megfigyelhető értéknél 50 nagyságrenddel nagyobb korrekció során alakul ki, ami nyilvánvalóan elfogadhatatlan. A megoldást itt Kaluza-Klein-modellek, szupergravitáció, sokdimenziós szupermembrán-elméletek felé keresik.

• 6. neutrínóprobléma vagy napneutrínó-probléma: az érvényes napmodellekhez képest a Földre a Napból a vártnál jóval kevesebb neutrínó érkezik, mintha a Nap energiatermelése az észleltnél jóval kisebb lenne, vagy valami történne a neutrínókkal útközben. A jelenlegi földi kísérletek az elektron-neutrínókat tudják érzékelni, azaz például ha ezek müon-neutrínókká tudnak átalakulni ún. neutrínóoszcilláció során, akkor magyarázni tudjuk a hiányt. Ehhez a standard modellel ellentétben a neutrínóknak tömeggel kell rendelkezniük. 1998-ban erre a Super-Kamiokande kísérlet bizonyítékot talált, s emiatt újabb 10 paramétert kell bevezetni a standard modellbe.

• 7. csatolási állandók problémája: a három kölcsönhatás csatolási állandói különbözőek, ami gátja az egyesítésnek, mert ahhoz egy univerzális csatolási állandóval kell rendelkezniük. Szerencsére a három csatolási állandó energiafüggő és 10¹⁵ GeV környékén értékük közel ugyanaz, ami azt jelzi, hogy ez a nagy egyesített elméletek skálája. Sajnos azonban nem egy, hanem három különböző pontban metszi egymást a három csatolási állandó, márpedig az egyesítéshez egy közös metszésponttal kellene rendelkezniük. A szuperszimmetrikus elméletek ezt a problémát megoldják.

• 8. sötét anyag problémája Az Univerzum anyagának többségét nem látjuk, csak a gravitációját érezzük. Mi lehet ez az anyag? Tömeges neutrínók? A legkönnyebb szuperszimmetrikus részecskék, amiket megmaradási törvény véd a bomlástól (R-paritás)? Valami egyéb?

Külső hivatkozások

• Horváth Dezső: A Standard Modell: mi az, és mire jó? Archiválva 2013. március 20-i dátummal a Wayback Machine-ben, Természet Világa nagyenergiás fizika különszám, 2000
• Balogh Vilmos Szilárd: Hopsz, itt a Higgs - avagy mégsem? Fizikai Nobel-díj 2013, Mérleg, 2013, 188-204. o. ,
• Elena Symeonidou és Nick Tracas: Az elemi részecskék színgazdag világa. Magyaríttott Flash prezentáció három játékkal (hadronépítés kvarkokból stb.)